I need to evaluate a function (say) Fxy = 2*x.^2 +3 *y.^2; on a ternary grid x-range (0 - 1), y-range (0-1) and 1-x-y (0 - 1). I am unable to construct the ternary grid on which I need to evaluate the above function. Also, once evaluated I need to plot the function in a ternary contour plot. Ideally, I need the axes to go counter clockwise in the sense (x -> y--> (1-x-y)).
I have tried the function
function tg = triangle_grid ( n, t )
ng = ( ( n + 1 ) * ( n + 2 ) ) / 2;
tg = zeros ( 2, ng );
p = 0;
for i = 0 : n
for j = 0 : n - i
k = n - i - j;
p = p + 1;
tg(1:2,p) = ( i * t(1:2,1) + j * t(1:2,2) + k * t(1:2,3) ) / n;
end
end
return
end
for the number of sub intervals between the triangle edge coordinates
n = 10 (say)
and for the edge coordinates of an equilateral triangle
t = tcoord = [0.0, 0.5, 1.0;
0.0, 1.0*sqrt(3)/2, 0.0];
This generated a triangular grid with the x-axis from 0-1 but the other two are not from 0-1.
I need something like this:
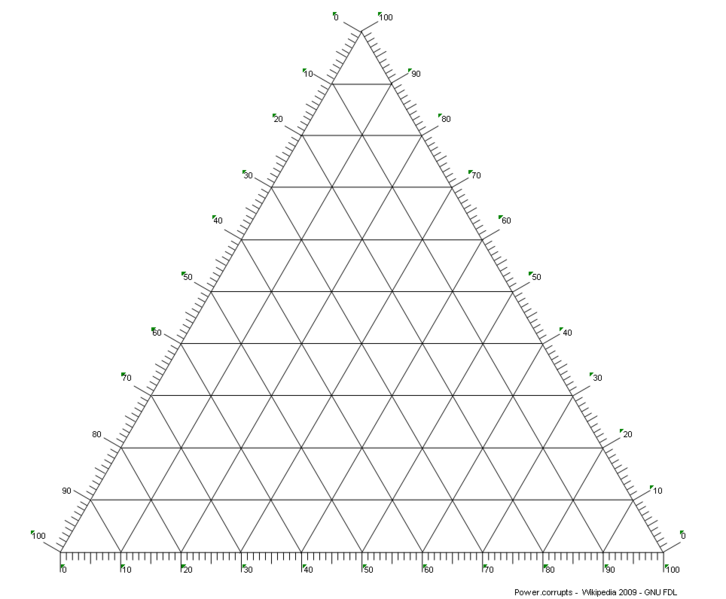
... with the axes range 0-1 (0-100 would also do).
In addition, I need to know the coordinate points for all intersections within the triangular grid. Once I have this I can proceed to evaluate the function in this grid.
My final aim is to get something like this. This is a better representation of what I need to achieve (as compared to the previous plot which I have now removed)
Note that the two ternary plots have iso-value contours which are different in in magnitude. In my case the difference is an order of magnitude, two very different Fxy's.
If I can plot the two ternary plots on top of each other then and evaluate the compositions at the intersection of two iso-value contours on the ternary plane. The compositions should be as read from the ternary plot and not the rectangular grid on which triangle is defined. Currently there are issues (as highlighted in the comments section, will update this once the problem is closer to solution).




I am the author of ternplot. As you have correctly surmised,
ternpcolordoes not do what you want, as it is built to grid data automatically. In retrospect, this was not a particularly wise decision, I've made a note to change the design. In the mean time this code should do what you want:EDIT: I've changed the code to find the intersection of two curves rather than just one.
EDIT 2: If you want to find the point of intersection between two contours, you are effectively solving two simultaneous equations. This bit of extra code will solve that for you (notice I've used some anonymous functions in the code above now, as well):